Числа Фибоначчи — одно из самых захватывающих и универсальных математических открытий, восходящее к началу XIII века. Этот ряд чисел был представлен итальянским математиком Леонардо Пизанским, известным как Фибоначчи, в его работе «Liber Abaci» (1202 год). Числа Фибоначчи играют значительную роль не только в математике, но и во многих других областях, включая компьютерные науки, биологию и искусство.
Определение
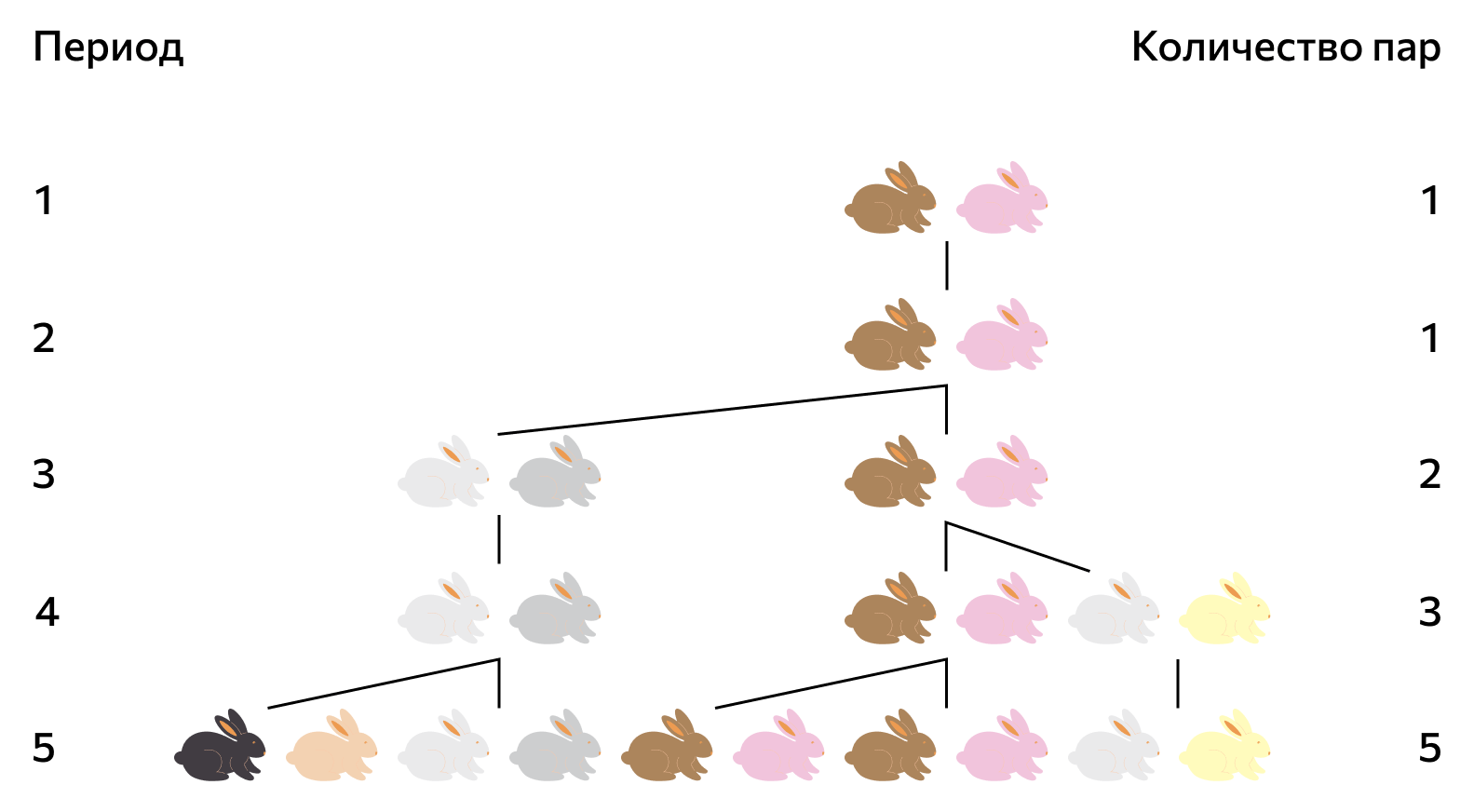
Последовательность Фибоначчи начинается с чисел 0 и 1, после чего каждое последующее число является суммой двух предыдущих. Таким образом, первые числа последовательности выглядят следующим образом: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Формально это можно выразить следующей формулой: F(n) = F(n-1) + F(n-2), где F(n) — n-ное число Фибоначчи.
Свойства и интересные факты
Числа Фибоначчи обладают множеством уникальных свойств и встречаются в самых неожиданных местах:
- Золотое сечение: Отношение последовательных чисел Фибоначчи приближается к золотому сечению (примерно 1.618033988749895…), которое считается идеалом гармонии в искусстве и архитектуре.
- Природа: Удивительно, но числа Фибоначчи можно найти в природе: расположение лепестков на цветке, распределение семян в подсолнечнике, количество чешуек на шишке — все эти явления следуют последовательности Фибоначчи.
- Теория чисел: Числа Фибоначчи используются в различных теоретических исследованиях, включая доказательство теорем и изучение свойств чисел.
Применение в современном мире
Компьютерные науки
В информатике последовательность Фибоначчи применяется в алгоритмах сортировки, поиска и оптимизации. Также она используется в теории игр, криптографии и для разработки программного обеспечения.
Криптография
Числа Фибоначчи находят применение в криптографии благодаря своим уникальным свойствам и способности генерировать псевдослучайные последовательности, что является важным элементом в создании шифров и кодов безопасности.
Биология и медицина
В биологии последовательность Фибоначчи помогает объяснить многие явления, такие как формирование спиралей в раковинах моллюсков, рост ветвей деревьев и расположение листьев. В медицине эти знания могут использоваться для анализа роста тканей и развития заболеваний.
Искусство и архитектура
Многие художники и архитекторы использовали золотое сечение, основанное на числах Фибоначчи, для создания гармоничных и эстетически приятных произведений. Это принцип можно найти в произведениях Леонардо да Винчи, Ле Корбюзье и других мастеров.
Заключение
Числа Фибоначчи продолжают вдохновлять ученых, инженеров, художников и многих других специалистов своей универсальностью и красотой. Отражая глубокую связь между математикой и природными явлениями, они подчеркивают взаимосвязь всех аспектов мира. В эпоху цифровизации и развития технологий понимание и применение чисел Фибоначчи открывает новые горизонты в научных исследованиях и практических разработках, демонстрируя, как древние знания могут найти свое место в современном мире.